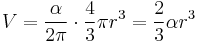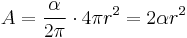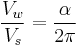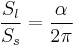Spherical wedge
In geometry, a spherical wedge or ungula is a portion of a ball bounded by two plane semidisks and a spherical lune (termed the wedge's base). The angle between the radii lying within the bounding semidisks is the dihedral angle of the wedge α. If AB is a semidisk that forms a ball when completely revolved about the z-axis, revolving AB only through a given α produces a spherical wedge of the same angle α.[1] Beman (2008)[2] remarks that "a spherical wedge is to the sphere of which it is a part as the angle of the wedge is to a perigon."[A] A spherical wedge of α = π radians (180°) is called a hemisphere, while a spherical wedge of α = 2π radians (360°) constitutes a complete ball.
The volume of a spherical wedge can be intuitively related to the AB definition in that while the volume of a ball of radius r is given by 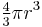 , the volume a spherical wedge of the same radius r is given by[3]
, the volume a spherical wedge of the same radius r is given by[3]
Extrapolating the same principle and considering that the surface area of a sphere is given by 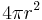 , it can be seen that the surface area of the lune corresponding to the same wedge is given by[A]
, it can be seen that the surface area of the lune corresponding to the same wedge is given by[A]
Hart (2009)[3] states that the "volume of a spherical wedge is to the volume of the sphere as the number of degrees in the [angle of the wedge] is to 360".[A] Hence, and through derivation of the spherical wedge volume formula, it can be concluded that, if 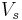 is the volume of the sphere and
is the volume of the sphere and 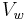 is the volume of a given spherical wedge,
is the volume of a given spherical wedge,
Also, if Sl is the area of a given wedge's lune, and Ss is the area of the wedge's sphere,[4][A]
See also
Notes
- A. ^ A distinction is sometimes drawn between the terms "sphere" and "ball", where a sphere is regarded as being merely the outer surface of a solid ball. It is common to use the terms interchangeably, as the commentaries of both Beman (2008) and Hart (2008) do.
References
- ^ P. Morton (1830). Geometry, plane, solid, and spherical, in six books. Baldwin and Cradock. p. 180.
- ^ D. W. Beman (2008). New Plane and Solid Geometry. BiblioBazaar, LLC. p. 338. ISBN 0554447010.
- ^ a b C. A. Hart (2009). Solid Geometry. BiblioBazaar, LLC. p. 465. ISBN 1103118048.
- ^ E. A. Avallone, T. Baumeister, A. Sadegh, L. S. Marks (2006). Marks' standard handbook for mechanical engineers. McGraw-Hill Professional. p. 43. ISBN 0071428674.